Центр Компьютерного Инжиниринга "Нумерика"
НЕЛИНЕЙНЫЙ ПЕРЕХОДНЫЙ ТЕПЛОВОЙ АНАЛИЗ ТЕМПЕРАТУР КОНСТРУКЦИЙ СУХОГО ДОКА ЗА 30-ЛЕТНИЙ ПЕРИОД
Специалисты ООО «ЦКИ «Нумерика» и НИЦ «Гидротекс» выполнили работы по численному моделированию хода температур конструкций сухого дока за 30-летний период. Работы выполнены в рамках научно-технического сопровождения проектирования объекта и позволили получить положительное заключение Главгосэкспертизы при назначении марки бетона по морозостойкости для буронабивных свай.
Дата: июль 2019 г.
Введение
Сухой док – гидротехническое сооружение, предназначенное для строительства, ремонта и обслуживания плавсредств. Внешне представляет собой бассейн, отделённый от акватории затвором (батопортом), с возможностью откачки заполнения водой.
Данная работа выполнялась в рамках программы научно-технического сопровождения проектирования объекта наряду с поверочными расчетами прочности днища сухого дока.
Данная работа выполнялась в рамках программы научно-технического сопровождения проектирования объекта наряду с поверочными расчетами прочности днища сухого дока.
Целью расчетных исследований, выполненных специалистами ООО «ЦКИ «Нумерика», является оценка требований по морозостойкости к бетону буронабивных свай сухого дока путем численного анализа температур оголовков свай с учетом изолирующего эффекта вышележащих конструкций и грунта.
https://marinetech.su/
https://marinetech.su/
Описание проблемы
Дальнейшее описание проекта частично повторяет публикацию авторов работы [20].
С помощью различных методик подбора состава бетонной смеси бетон можно адаптировать к различным условиям окружающей среды, в том числе и к наиболее суровому климату [3, 6]. В связи с этим в настоящее время существует ряд нормативных документов, регламентирующих требуемую марку бетона по морозостойкости для различных типов конструкций в зависимости от расчётной температуры наружного воздуха и различных условий эксплуатации [2, 5, 10–16]. Однако существует достаточно большая группа заглубленных в грунт или подземных инженерных сооружений, конструкции которых не имеют непосредственного контакта с наружным воздухом и не подвергаются инсоляции. Для таких сооружений температура конструкций определяется их теплотехническими свойствами и температурным режимом окружающего грунта. При этом отдельными нормами [11, 15] хотя и предъявляются некоторые требования по морозостойкости к бетону таких конструкций, но регулирующими параметрами всё так же являются температура наружного воздуха и условия эксплуатации.
С помощью различных методик подбора состава бетонной смеси бетон можно адаптировать к различным условиям окружающей среды, в том числе и к наиболее суровому климату [3, 6]. В связи с этим в настоящее время существует ряд нормативных документов, регламентирующих требуемую марку бетона по морозостойкости для различных типов конструкций в зависимости от расчётной температуры наружного воздуха и различных условий эксплуатации [2, 5, 10–16]. Однако существует достаточно большая группа заглубленных в грунт или подземных инженерных сооружений, конструкции которых не имеют непосредственного контакта с наружным воздухом и не подвергаются инсоляции. Для таких сооружений температура конструкций определяется их теплотехническими свойствами и температурным режимом окружающего грунта. При этом отдельными нормами [11, 15] хотя и предъявляются некоторые требования по морозостойкости к бетону таких конструкций, но регулирующими параметрами всё так же являются температура наружного воздуха и условия эксплуатации.

Марка бетона по морозостойкости показывает число циклов замораживания и оттаивания в состоянии насыщения влагой, при которых прочность бетона сохраняется в нормируемых пределах и отсутствуют внешние признаки разрушения. Число циклов замораживания-оттаивания связано с количеством переходов температуры бетонной конструкции через значение температуры замерзания воды (обычно 0 °С).
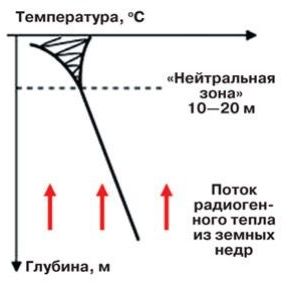
Если для конструкций, контактирующих с наружным воздухом, количество таких переходов сильно зависит от количества переходов температуры воздуха через 0 °С и интенсивности инсоляции, то для заглубленных в грунт сооружений может наблюдаться другая картина. Амплитуда колебаний температур грунта быстро падает с увеличением глубины. Это обусловлено в основном изолирующим эффектом вышележащих слоев. Соответственно, на некоторой глубине количество переходов температуры через 0 °С будет значительно меньше, чем на поверхности, а значит, требования по морозостойкости к бетону можно снизить. Изолирующий эффект могут оказывать также вышележащие конструкции зданий и сооружений.
Обсуждений в научной литературе вопроса о назначении марки бетона заглубленных в грунт технологически независимых конструкций в такой постановке в ходе анализа литературы обнаружено не было.
В соответствии с этим в данной работе специалисты ЦКИ «Нумерика» и НИЦ «Гидротекс» впервые предложили и применили принцип назначения требований к бетону по морозостойкости путём численного анализа температурного режима конструктивных элементов сооружения с учетом изолирующего эффекта вышележащих конструкций и грунта.
В соответствии с этим в данной работе специалисты ЦКИ «Нумерика» и НИЦ «Гидротекс» впервые предложили и применили принцип назначения требований к бетону по морозостойкости путём численного анализа температурного режима конструктивных элементов сооружения с учетом изолирующего эффекта вышележащих конструкций и грунта.
Для достижения поставленной цели в данной работе рассчитан температурный режим свайного основания и плиты свайного ростверка за 30-летний период с 1989 по 2018 гг. Переходный тепловой анализ выполнен в физически нелинейной постановке, учитывающей изменение теплофизических характеристик грунта в зависимости от его температуры. На примере данного расчета показано, что требуемая марка бетона по морозостойкости, применяемого для свай, в определенных условиях может быть снижена.
Постановка задачи
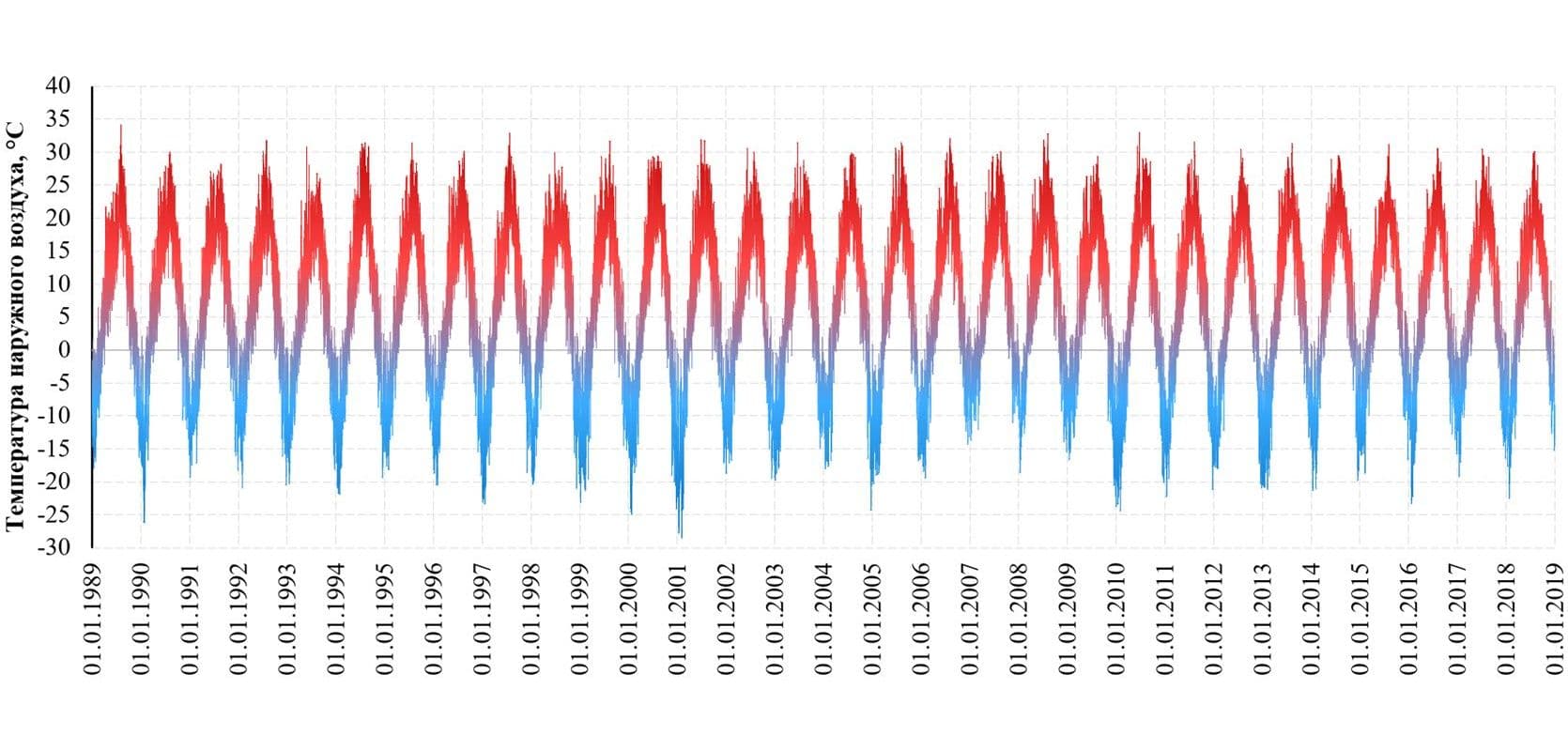
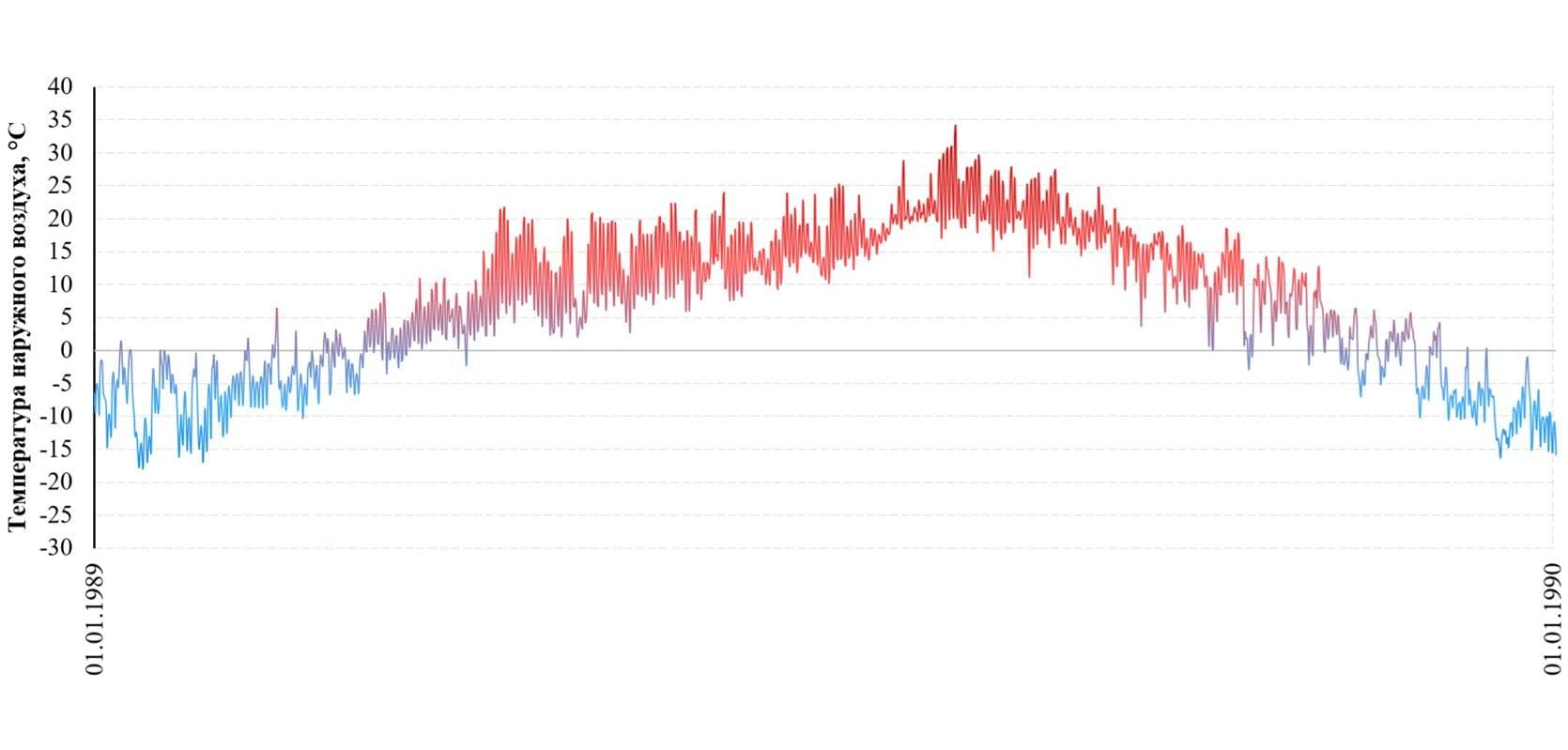
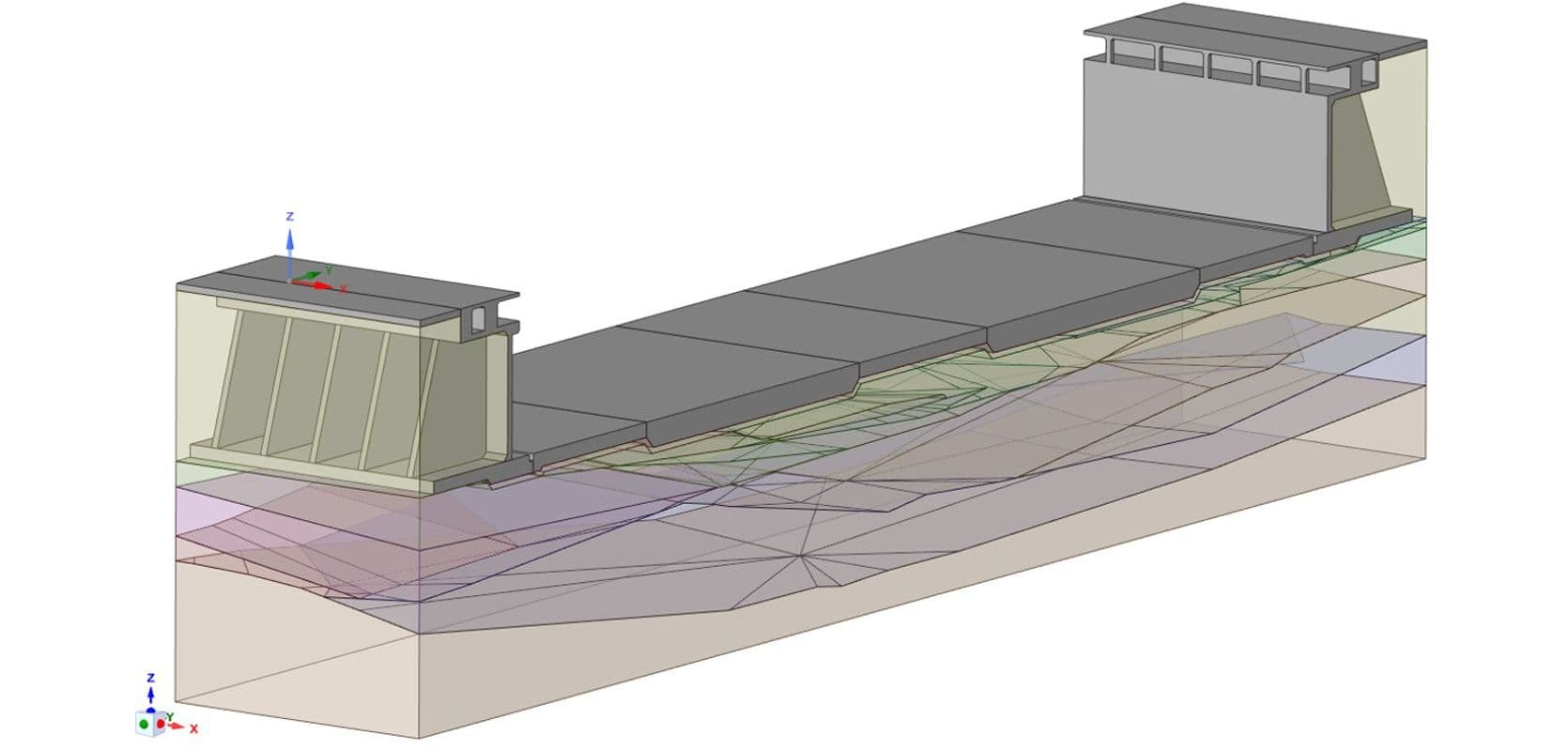
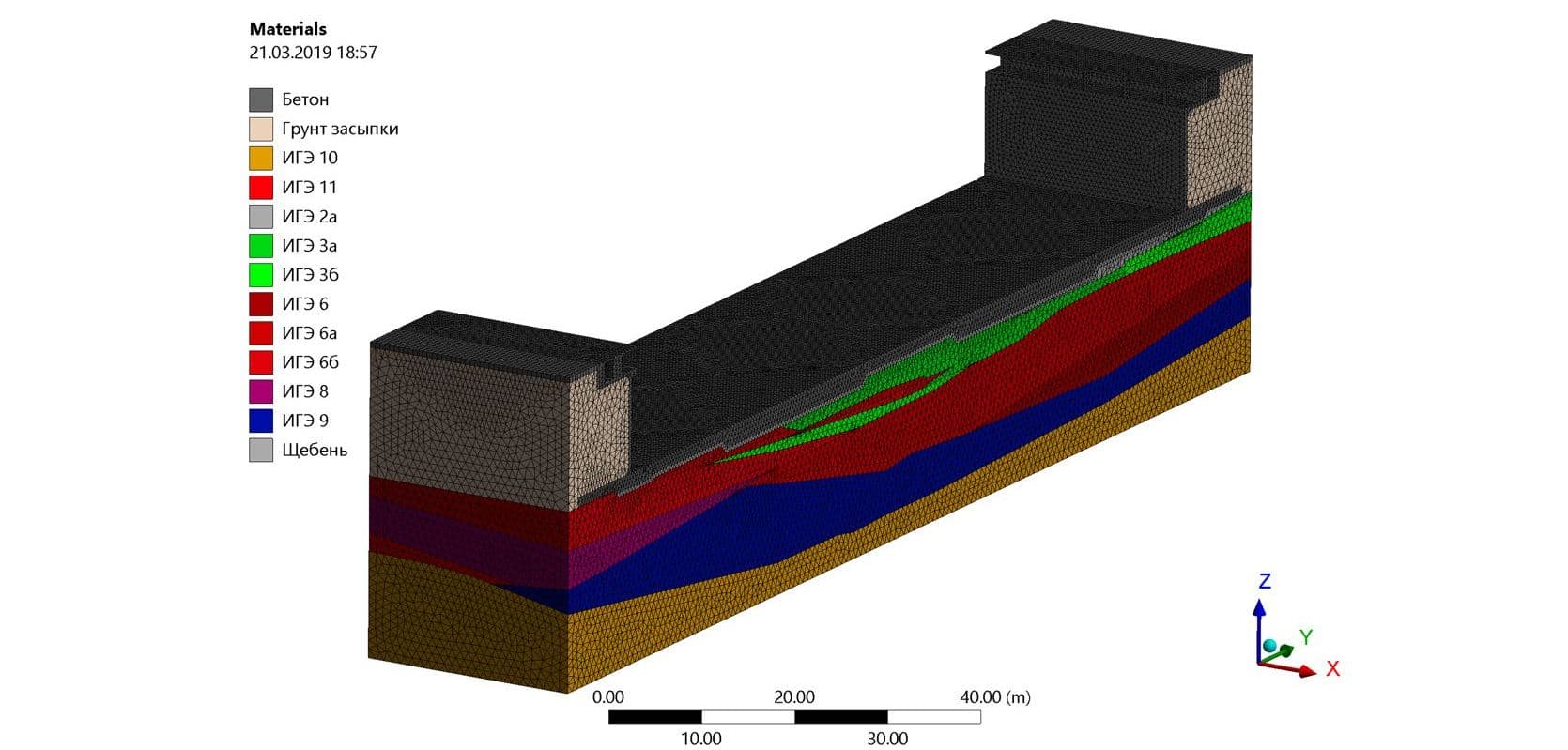
Расчет температурных полей конструкций днища сухого дока выполнен в программном комплексе конечно-элементного анализа ANSYS. В качестве исходных данных использовался ряд наблюдений температур воздуха в месте расположения объекта с 1989 по 2018 гг. Расчеты выполнены в физически нелинейной постановке, учитывающей изменение теплофизических характеристик геологических элементов в зависимости от температуры. На первом этапе выполнен расчет секции сухого дока с учетом влияния теплового потока со стороны стен дока и геологических слоев выбранного участка. На втором этапе производился уточняющий расчет фрагмента секции – центральной плиты «легкой» зоны.
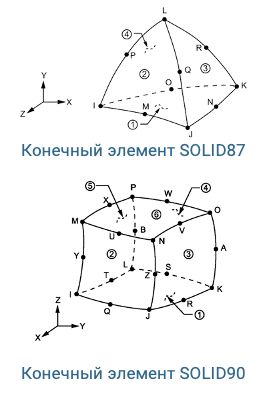
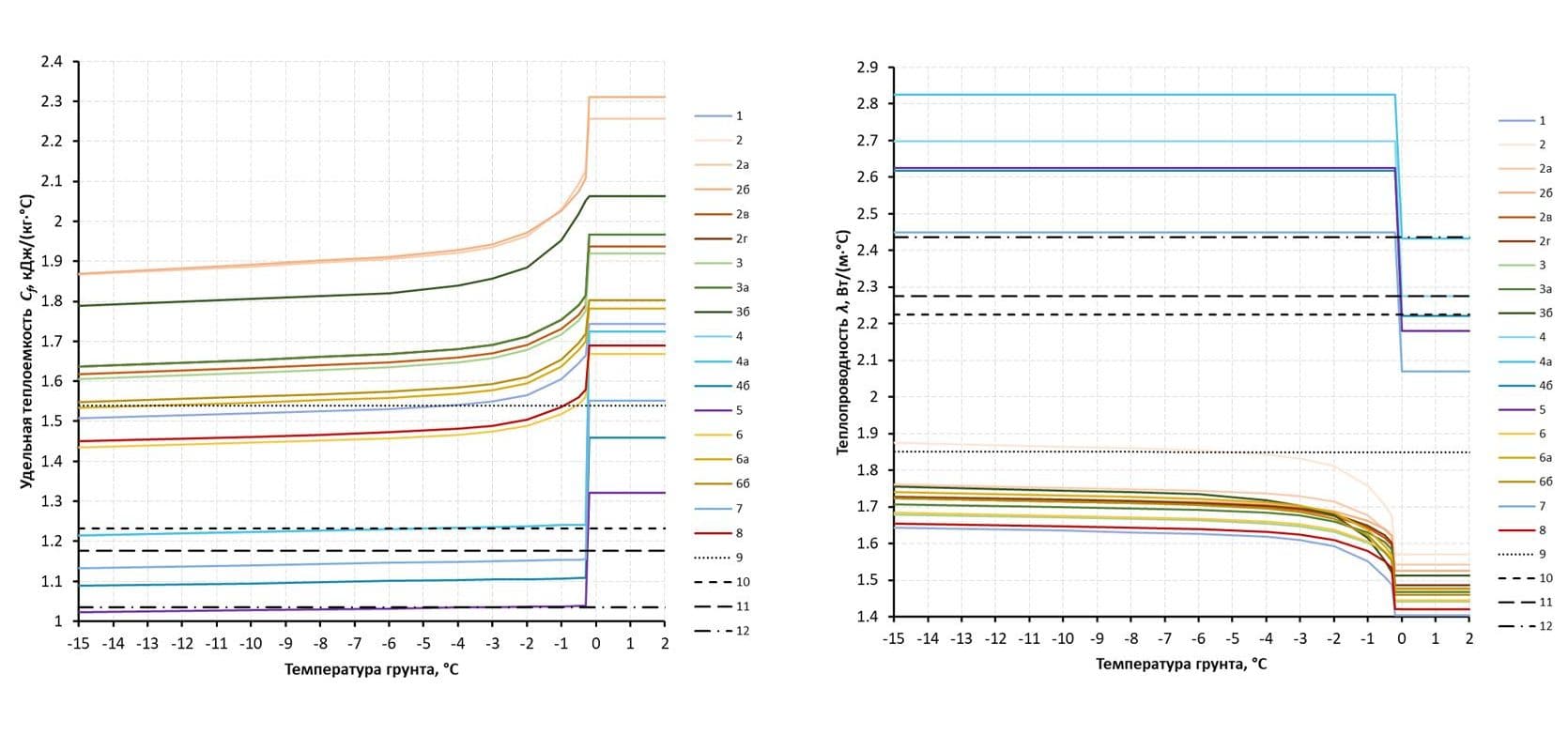
Теплофизические характеристики бетона приняты согласно приложению Б СП 41.13330.2012 «Бетонные и железобетонные конструкции гидротехнических сооружений» [14]. Теплофизические нелинейные характеристики грунта определены согласно приложению Б СП 25.13330.2012 «Основания и фундаменты на вечномерзлых грунтах» [9] на основе таких физико-механических характеристик, как плотность грунта ρ, естественная влажность w, коэффициент пористости e, число пластичности IP и показатель текучести IL.
На боковых гранях численной модели задается граничное условие II рода, характеризуемое нулевым тепловым потоком через боковые грани (q = 0).
Предполагается что нижняя граница массива грунта является слоем нулевых градиентов температур (слоем постоянной годовой температуры), т.е. температура данного слоя грунта неизменна на протяжении года. Температура данного слоя равна среднегодовой температуре воздуха в исследуемом районе, что подтверждается некоторыми авторами [5, 6]. Соответственно к нижней грани численной модели прикладывается граничное условие I рода – постоянная температура равная среднегодовой температуре наружного воздуха
Начальная температура системы принималась равной среднемесячной температуре марта (месяц начала расчёта). Среднемесячная температура марта совпадает со среднегодовой температурой воздуха.
Главное матричное уравнение в нестационарном (переходном) нелинейном тепловом анализе записывается как
[ C ( T ) ] { T' } + [ K ( T ) ] { T } = { Q ( T , t ) }
где [ C ( T ) ] и [ K ( T ) ] – зависимые от состояния системы (температур) матрицы удельной теплоемкости и теплопроводности соответственно; { T } – вектор температур; { Q ( T , t ) } – зависимый от температур и времени эквивалентный узловой вектор теплового потока (вектор внешних «нагрузок»).
Для решения систем нелинейных уравнений применяется итерационный метод сопряжённых градиентов с предобусловленностью. Предобуславливатель строится на основе разложения Холецкого, т.е. представления симметричной положительно-определённой матрицы A в виде A = LLT, где L – нижняя треугольная матрица со строго положительными элементами на диагонали; либо в эквивалентной форме: A=UTU, где U=LT – верхняя треугольная матрица.
Предполагается что нижняя граница массива грунта является слоем нулевых градиентов температур (слоем постоянной годовой температуры), т.е. температура данного слоя грунта неизменна на протяжении года. Температура данного слоя равна среднегодовой температуре воздуха в исследуемом районе, что подтверждается некоторыми авторами [5, 6]. Соответственно к нижней грани численной модели прикладывается граничное условие I рода – постоянная температура равная среднегодовой температуре наружного воздуха
t(ср.год) = 6,66°С.
Начальная температура системы принималась равной среднемесячной температуре марта (месяц начала расчёта). Среднемесячная температура марта совпадает со среднегодовой температурой воздуха.
Главное матричное уравнение в нестационарном (переходном) нелинейном тепловом анализе записывается как
[ C ( T ) ] { T' } + [ K ( T ) ] { T } = { Q ( T , t ) }
где [ C ( T ) ] и [ K ( T ) ] – зависимые от состояния системы (температур) матрицы удельной теплоемкости и теплопроводности соответственно; { T } – вектор температур; { Q ( T , t ) } – зависимый от температур и времени эквивалентный узловой вектор теплового потока (вектор внешних «нагрузок»).
Для решения систем нелинейных уравнений применяется итерационный метод сопряжённых градиентов с предобусловленностью. Предобуславливатель строится на основе разложения Холецкого, т.е. представления симметричной положительно-определённой матрицы A в виде A = LLT, где L – нижняя треугольная матрица со строго положительными элементами на диагонали; либо в эквивалентной форме: A=UTU, где U=LT – верхняя треугольная матрица.
Анализ результатов расчета
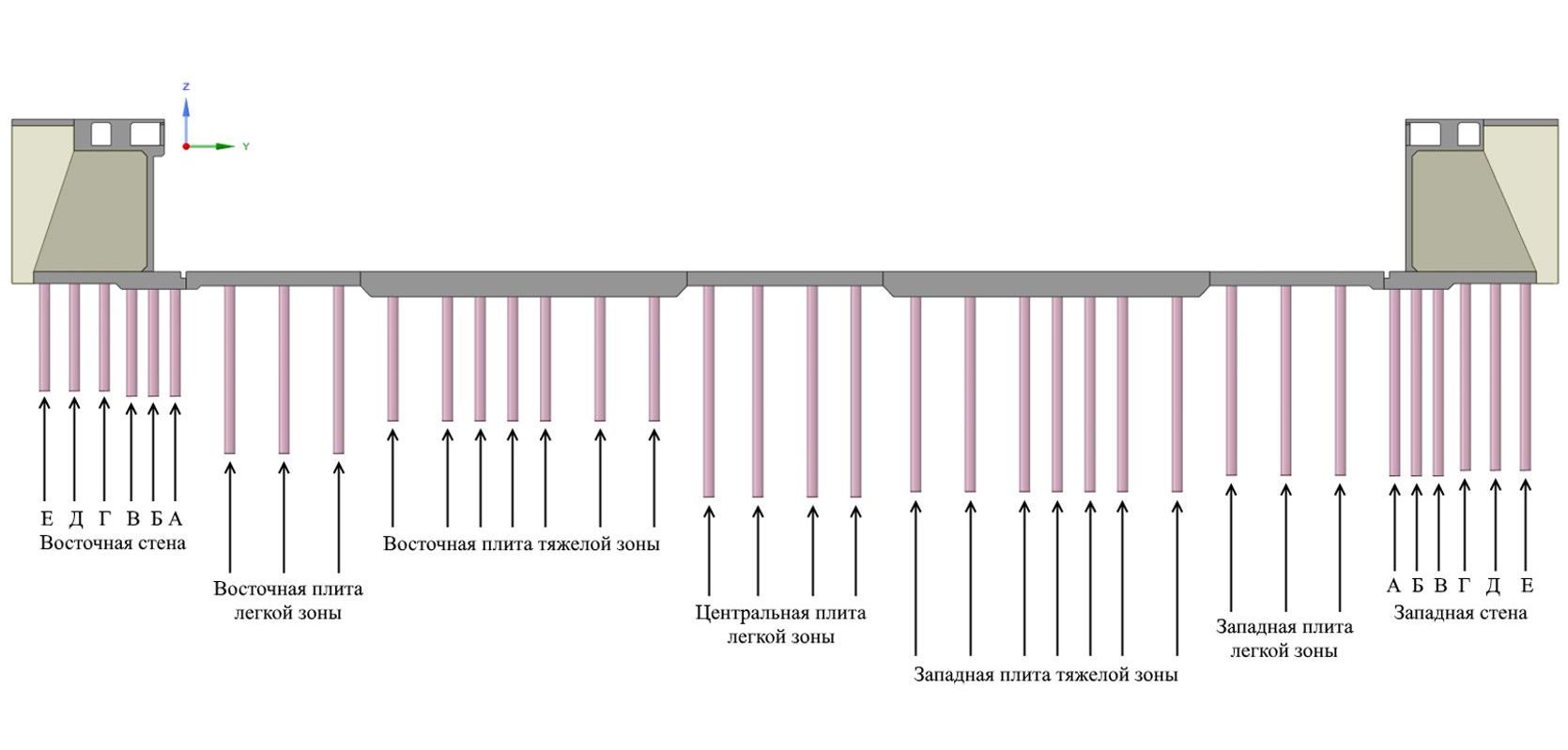
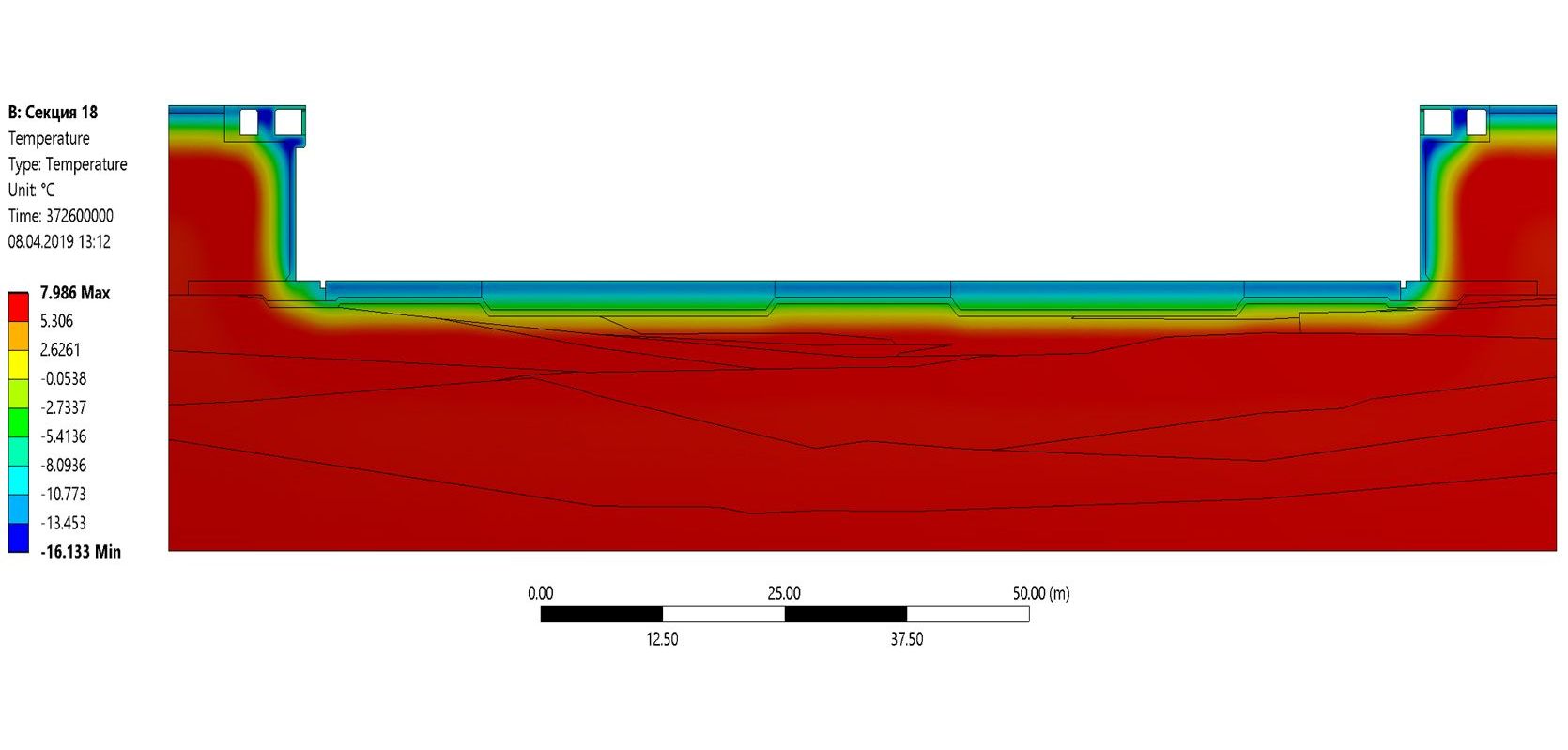
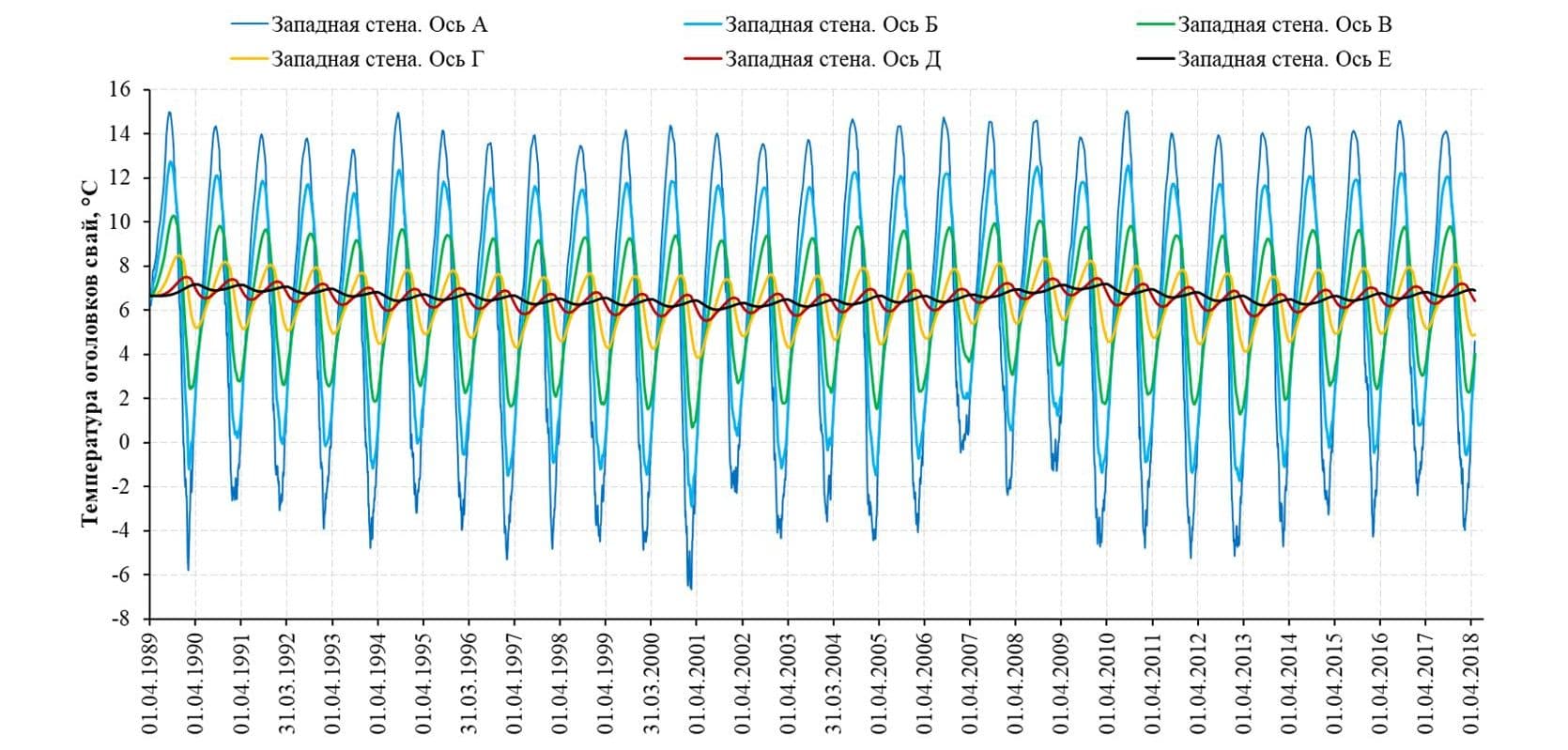
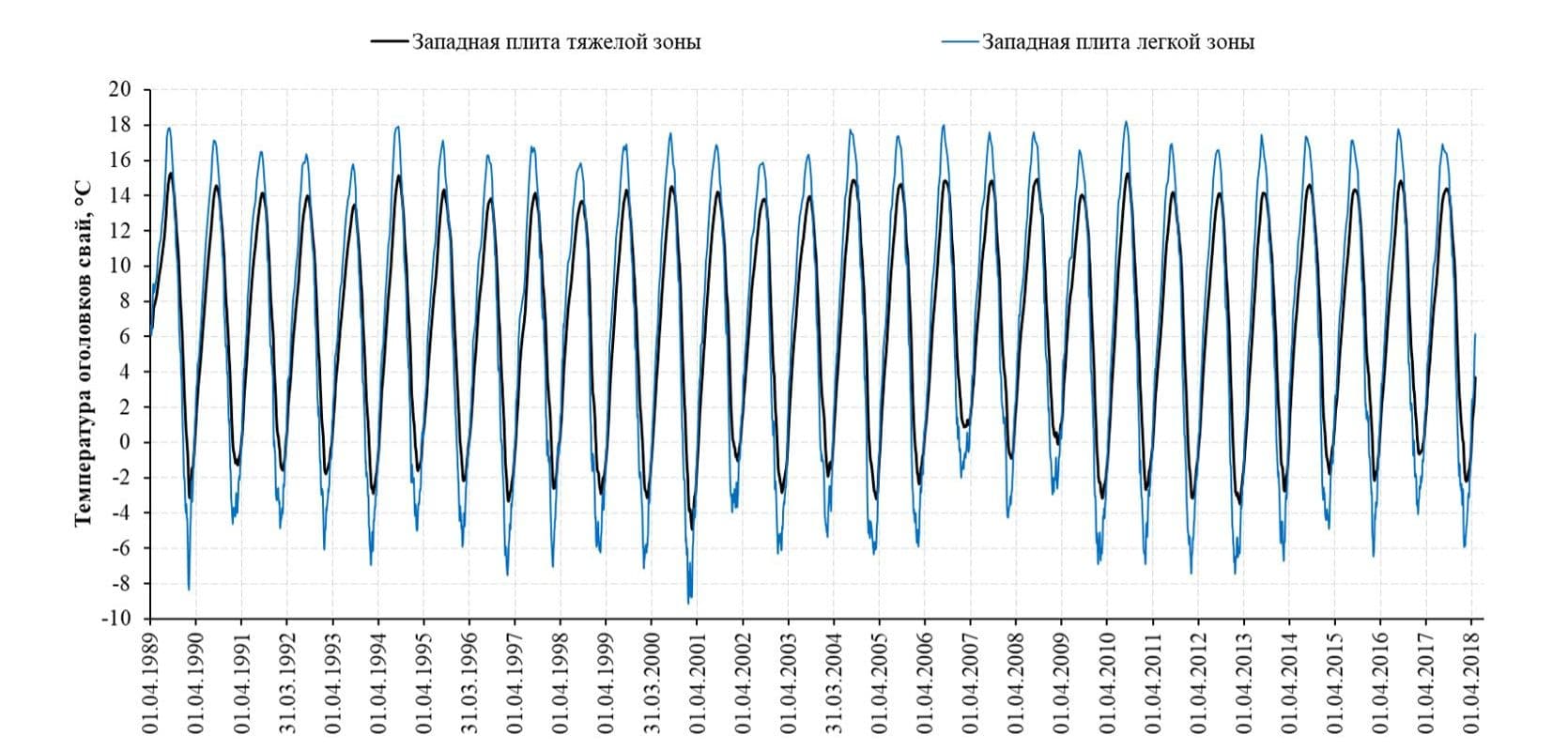
Время расчета модели составило 7 дней. В результате расчета был определен ход температур в каждой точке модели, в частности – в оголовках свай каждого ряда. Результаты показали значительное уменьшение амплитуд температур для рядов свай, подверженных отепляющему воздействию окружающего грунта в районе стен секции сухого дока.
Уменьшение амплитуд температур свай под плитами дока менее существенно. Тем не менее расчетные минимальные температуры оголовков свай значительно выше минимальных температур окружающего воздуха. Таким образом, подтверждается возможность назначения марки по морозостойкости для бетона свай в зависимости от фактических температур конструктивных элементов, а не от температур наружного воздуха.
Результаты расчета были проанализированы и обработаны тремя методами для определения температуры оголовков свай наиболее холодной пятидневки обеспеченностью 92%, необходимой для назначения марки бетона по морозостойкости в соответствии с требованиями нормативных документов. Построены интегральные кривые обеспеченности температур наиболее холодной пятидневки.
Метод №1. Температура оголовков свай наиболее холодной пятидневки обеспеченностью 92% определяется согласно методике, описанной в приложении Б СП 131.13330.2018 Строительная климатология [17], как для температуры воздуха наиболее холодной пятидневки. Ряд температур ранжируется в порядке убывания абсолютных значений метеорологической величины. Каждому значению присваивается порядковый номер, а его повторяемость Pm, %, определяется по формуле Н.Н. Чегодаева:
Метод №1. Температура оголовков свай наиболее холодной пятидневки обеспеченностью 92% определяется согласно методике, описанной в приложении Б СП 131.13330.2018 Строительная климатология [17], как для температуры воздуха наиболее холодной пятидневки. Ряд температур ранжируется в порядке убывания абсолютных значений метеорологической величины. Каждому значению присваивается порядковый номер, а его повторяемость Pm, %, определяется по формуле Н.Н. Чегодаева:
где m – порядковый номер; n – число членов ранжированного ряда.
Значение температуры наиболее холодной пятидневки заданной обеспеченности определяется методом интерполяции по интегральной кривой распределения температуры наиболее холодной пятидневки, построенной на вероятностной сетчатке. Для оси ординат используется логарифмическая шкала температуры воздуха, для оси абсцисс – двойная логарифмическая шкала обеспеченности.
Метод №2. Температура низа плит наиболее холодной пятидневки обеспеченностью 92% определяется согласно методике, описанной в «Справочное пособие к СНиП 23-01-99* Строительная климатология [19]. Ряд температур ранжируется в порядке убывания абсолютных значений метеорологической величины. Каждому значению присваивается порядковый номер. Значения температур округляются до 0,5 °С с присвоением среднего порядкового номера. Обеспеченность температуры определяется по формуле (4.1). Дальнейшие действия аналогичны методу №1.
Метод №3. Данный метод предполагает использование распределения экстремальных значений Фишера-Типпета I типа (закон распределения Гумбеля – двойное экспоненциальное распределение). Закон распределения Гумбеля используется в случае, когда в качестве случайной величины рассматриваются экстремальные характеристики гидрометеорологического режима. Функция обеспеченности Гумбеля определяется выражениями
Значение температуры наиболее холодной пятидневки заданной обеспеченности определяется методом интерполяции по интегральной кривой распределения температуры наиболее холодной пятидневки, построенной на вероятностной сетчатке. Для оси ординат используется логарифмическая шкала температуры воздуха, для оси абсцисс – двойная логарифмическая шкала обеспеченности.
Метод №2. Температура низа плит наиболее холодной пятидневки обеспеченностью 92% определяется согласно методике, описанной в «Справочное пособие к СНиП 23-01-99* Строительная климатология [19]. Ряд температур ранжируется в порядке убывания абсолютных значений метеорологической величины. Каждому значению присваивается порядковый номер. Значения температур округляются до 0,5 °С с присвоением среднего порядкового номера. Обеспеченность температуры определяется по формуле (4.1). Дальнейшие действия аналогичны методу №1.
Метод №3. Данный метод предполагает использование распределения экстремальных значений Фишера-Типпета I типа (закон распределения Гумбеля – двойное экспоненциальное распределение). Закон распределения Гумбеля используется в случае, когда в качестве случайной величины рассматриваются экстремальные характеристики гидрометеорологического режима. Функция обеспеченности Гумбеля определяется выражениями
где y – безразмерная величина, q – мода случайной величины X; x ̅ – среднее значение исходного ряда; γ ≈ 0,57722 – постоянная Эйлера-Маскерони; σx – среднеквадратичное отклонение исходного ряда выборки.
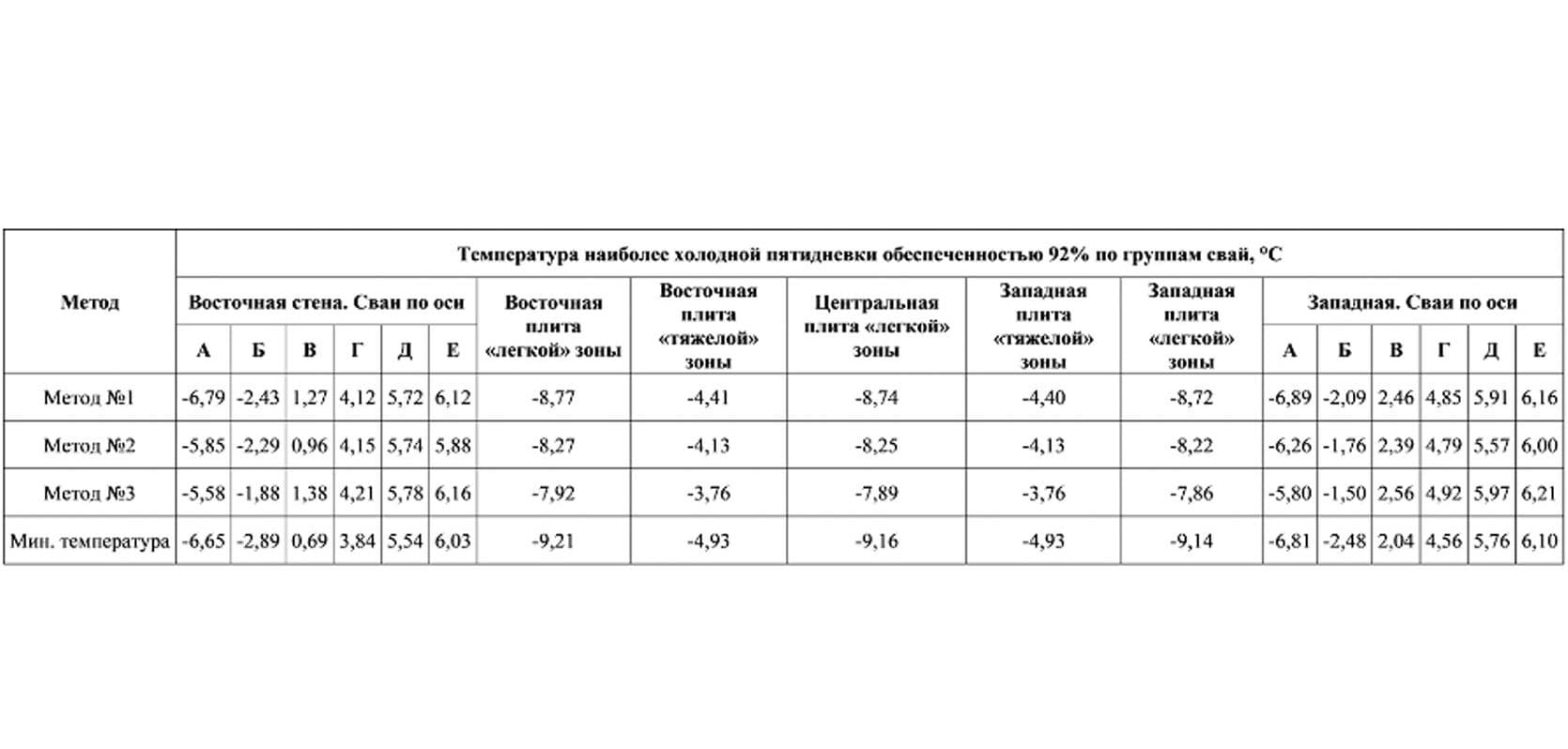
Температуры наиболее холодных пятидневок обеспеченностью 92% оголовков буронабивных свай, полученные в результате обработки результатов теплотехнического расчёта секции сухого дока, приведены в таблице ниже.
Температуры наиболее холодных пятидневок обеспеченностью 92% оголовков буронабивных свай, полученные в результате обработки результатов теплотехнического расчёта секции сухого дока, приведены в таблице ниже.
Рекомендуемые марки бетона по морозостойкости назначены в соответствии с таблицей Е.1 ГОСТ 31384-2017. Защита бетонных и железобетонных конструкций от коррозии [2] и таблицей Ж.1 [10] СП 28.13330.2017. Защита строительных конструкций от коррозии.
Таблица выше показывает, что для технологически независимых элементов конструкции могут быть назначены различные требования по морозостойкости. В данном примере для свай под плитой толщиной 1,3 м (с учетом бетонной подготовки) требуемая марка бетона по морозостойкости ниже на 1 ступень, а для свай под плитой толщиной 2,3 м ниже на 2 ступени, чем у железобетонной плиты, контактирующей с наружным воздухом. Необходимо отметить, что в данном примере не учитывалось влияние солнечной радиации на температурный режим конструкции. Поступление тепла от излучения также может способствовать нагреву поверхности плит и повышению расчетных температур элементов конструкций [4].
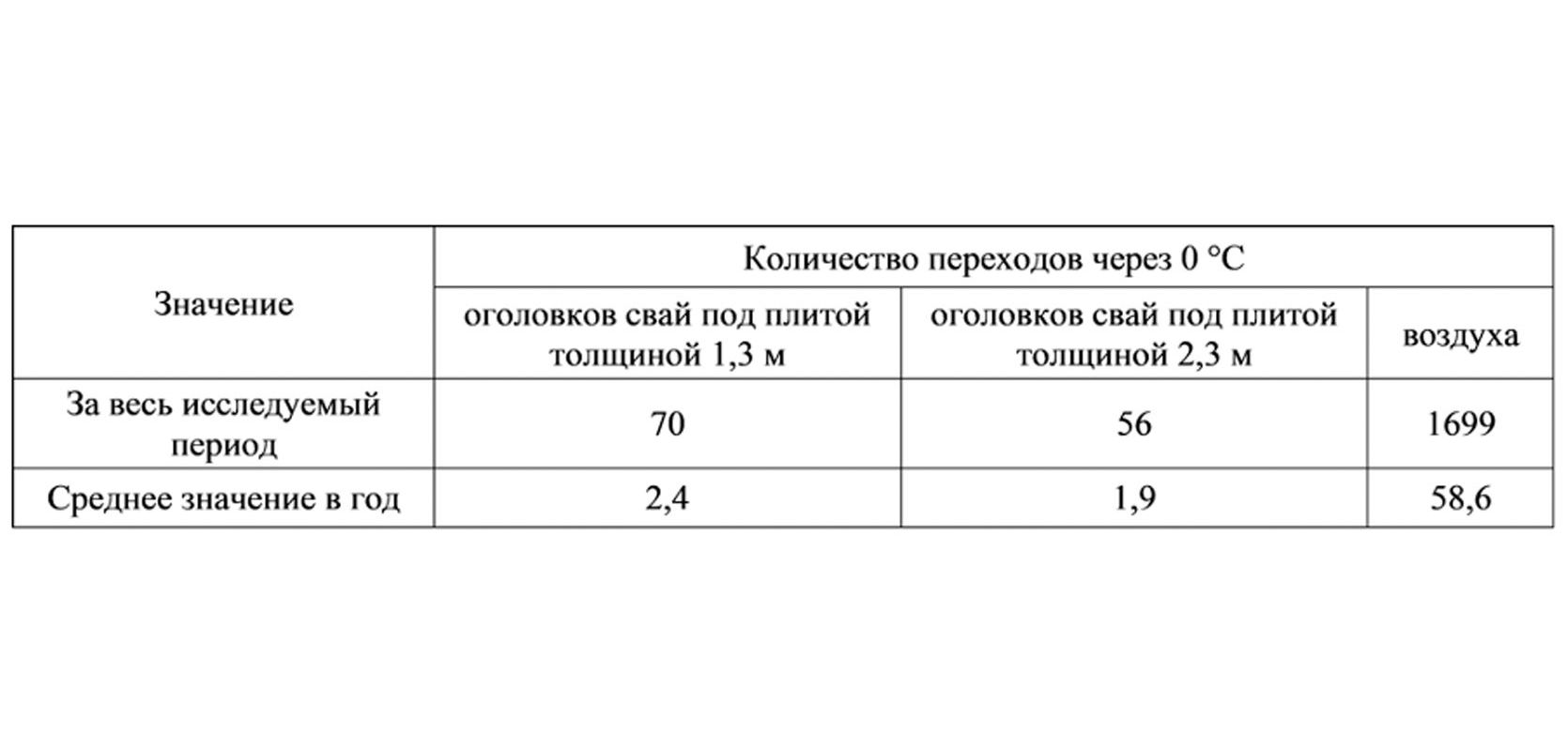
Кроме того, было рассчитано количество переходов температуры оголовков свай и воздуха через 0 °С (табл. 3), которое определялось количеством дней, когда максимальная температура положительна, а минимальная – отрицательна. Основываясь на полученных данных, можно заключить, что отепляющее воздействие грунта и вышележащих конструкций не только повышает минимальные температуры в сваях, но и значительно уменьшает количество циклов замораживания-оттаивания бетона в период эксплуатации конструкции.
Кроме того, было рассчитано количество переходов температуры оголовков свай и воздуха через 0 °С (табл. 3), которое определялось количеством дней, когда максимальная температура положительна, а минимальная – отрицательна. Основываясь на полученных данных, можно заключить, что отепляющее воздействие грунта и вышележащих конструкций не только повышает минимальные температуры в сваях, но и значительно уменьшает количество циклов замораживания-оттаивания бетона в период эксплуатации конструкции.
Заключение
В данной работе выполнен нелинейный переходный тепловой анализ конструкций сухого дока за период 30 лет. В результате проведенного расчетного исследования были сделаны следующие выводы:
1. Отсутствие контакта с наружным воздухом и наличие изолирующего эффекта от вышележащих конструкций и грунта значительно уменьшают количество переходов температуры бетона через значение 0 °С и, соответственно, циклов замораживания-оттаивания.
2. При решении практических задач целесообразно определять температурный режим заглубленных в грунт конструкций, но только в случае, если они имеют технологически независимые элементы. Таким образом, можно снизить требования к бетону, назначив марку бетона по морозостойкости для отдельных элементов конструкции по их наихудшим условиям эксплуатации.
3. Численное моделирование позволяет провести оценку требований к бетону по морозостойкости в зависимости от температур бетона. Рассмотренные методы использованы на практике для обоснования требований по морозостойкости к бетону различных конструкций, что в перспективе позволит получить положительный экономический эффект.
Список источников
1. Васильев Г.П. Теплохладоснабжение зданий и сооружений с использованием низкопотенциальной тепловой энергии поверхностных слоев земли. М.: Граница, 2006. 173 с.
2. ГОСТ 31384-2017. Защита бетонных и железобетонных конструкций от коррозии. Общие технические требования.
3. Исаченко С.Л., Кодзоев М.-Б.Х. Анализ методов повышения морозостойкости бетона // Бюллетень науки и практики. 2018. Т. 4, № 4. С. 291–294.
4. Кондратьев В.Г., Перекупка А.Г., Примаков С.С., Петрова А.С. Мероприятия по изменению режима теплообмена на поверхности земли и их влияние на распределение температуры в грунте // Нефтяное хозяйство. 2012. № 10. С. 122–125.
5. Малюк В.Д. О нормировании требований по морозостойкости бетона для морских сооружений // Транспортное строительство. 2010. № 3. С. 32–34.
6. Моргун А.Н. Морозостойкость бетона, способы ее повышения // Наука, техника и образование. 2015. № 7(13). С. 101–105.
7. Савин В.К. Строительная физика: энергоперенос, энергоэффективность, энергосбережение. М.: Лазурь, 2005. 432 с.
8. Сикан А.В. Методы статистической обработки гидрометеорологической информации. СПб.: РГГМУ, 2007. 279 с.
9. СП 25.13330.2012. Основания и фундаменты на вечномерзлых грунтах. Актуализированная редакция СНиП 2.02.04-88.
10. СП 28.13330.2017. Защита строительных конструкций от коррозии. Актуализированная редакция СНиП 2.03.11-85 (с Изменением N 1).
11. СП 31.13330.2012. Водоснабжение. Наружные сети и сооружения. Актуализированная редакция СНиП 2.04.02-84 (с Изменениями N 1, 2, 3).
12. СП 34.13330.2012. Автомобильные дороги. Актуализированная редакция СНиП 2.05.02-85*
(с Изменением N 1).
13. СП 35.13330.2011 Мосты и трубы. Актуализированная редакция СНиП 2.05.03-84*
(с Изменением N 1).
14. СП 41.13330.2012. Бетонные и железобетонные конструкции гидротехнических сооружений. Актуализированная редакция СНиП 2.06.08-87.
15. СП 120.13330.2012. Метрополитены. Актуализированная редакция СНиП 32-02-2003 (с Изменениями N 1, 2).
16. СП 121.13330.2012. Аэродромы. Актуализированная редакция СНиП 32-03-96.
17. СП 131.13330.2018. «СНиП 23-01-99*. Строительная климатология».
18. Чудновский А.Ф. Теплофизика почв. М.: Наука, 1976. 353 с.
19. Справочное пособие к СНиП 23-01-99* Строительная климатология/ Под редакцией члена-корр. Савина В.К. – М.: НИИ строительной физики РААСН, 2006 – 258 с.
20. Беккер A. Т, Помников E. Е, Макаров О. А. К оценке требований к бетону по морозостойкости в зависимости от температурного режима конструкций [Журнал] // Вестник Инженерной школы ДВФУ. - Владивосток, 2019 г. - 40: Т. 3. - стр. 143-153. DOI: https://dx.doi.org/10.24866/2227-6858/2019-3-15
2. ГОСТ 31384-2017. Защита бетонных и железобетонных конструкций от коррозии. Общие технические требования.
3. Исаченко С.Л., Кодзоев М.-Б.Х. Анализ методов повышения морозостойкости бетона // Бюллетень науки и практики. 2018. Т. 4, № 4. С. 291–294.
4. Кондратьев В.Г., Перекупка А.Г., Примаков С.С., Петрова А.С. Мероприятия по изменению режима теплообмена на поверхности земли и их влияние на распределение температуры в грунте // Нефтяное хозяйство. 2012. № 10. С. 122–125.
5. Малюк В.Д. О нормировании требований по морозостойкости бетона для морских сооружений // Транспортное строительство. 2010. № 3. С. 32–34.
6. Моргун А.Н. Морозостойкость бетона, способы ее повышения // Наука, техника и образование. 2015. № 7(13). С. 101–105.
7. Савин В.К. Строительная физика: энергоперенос, энергоэффективность, энергосбережение. М.: Лазурь, 2005. 432 с.
8. Сикан А.В. Методы статистической обработки гидрометеорологической информации. СПб.: РГГМУ, 2007. 279 с.
9. СП 25.13330.2012. Основания и фундаменты на вечномерзлых грунтах. Актуализированная редакция СНиП 2.02.04-88.
10. СП 28.13330.2017. Защита строительных конструкций от коррозии. Актуализированная редакция СНиП 2.03.11-85 (с Изменением N 1).
11. СП 31.13330.2012. Водоснабжение. Наружные сети и сооружения. Актуализированная редакция СНиП 2.04.02-84 (с Изменениями N 1, 2, 3).
12. СП 34.13330.2012. Автомобильные дороги. Актуализированная редакция СНиП 2.05.02-85*
(с Изменением N 1).
13. СП 35.13330.2011 Мосты и трубы. Актуализированная редакция СНиП 2.05.03-84*
(с Изменением N 1).
14. СП 41.13330.2012. Бетонные и железобетонные конструкции гидротехнических сооружений. Актуализированная редакция СНиП 2.06.08-87.
15. СП 120.13330.2012. Метрополитены. Актуализированная редакция СНиП 32-02-2003 (с Изменениями N 1, 2).
16. СП 121.13330.2012. Аэродромы. Актуализированная редакция СНиП 32-03-96.
17. СП 131.13330.2018. «СНиП 23-01-99*. Строительная климатология».
18. Чудновский А.Ф. Теплофизика почв. М.: Наука, 1976. 353 с.
19. Справочное пособие к СНиП 23-01-99* Строительная климатология/ Под редакцией члена-корр. Савина В.К. – М.: НИИ строительной физики РААСН, 2006 – 258 с.
20. Беккер A. Т, Помников E. Е, Макаров О. А. К оценке требований к бетону по морозостойкости в зависимости от температурного режима конструкций [Журнал] // Вестник Инженерной школы ДВФУ. - Владивосток, 2019 г. - 40: Т. 3. - стр. 143-153. DOI: https://dx.doi.org/10.24866/2227-6858/2019-3-15